Day 1 - Container With Most Water
An array problem for interview
Hello,
Welcome to the Day 1 of DSA, the problem statement for today goes as follow,
Given n non-negative integers a1, a2, ..., an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.
Notice that you may not slant the container.
Example 1:
Input:
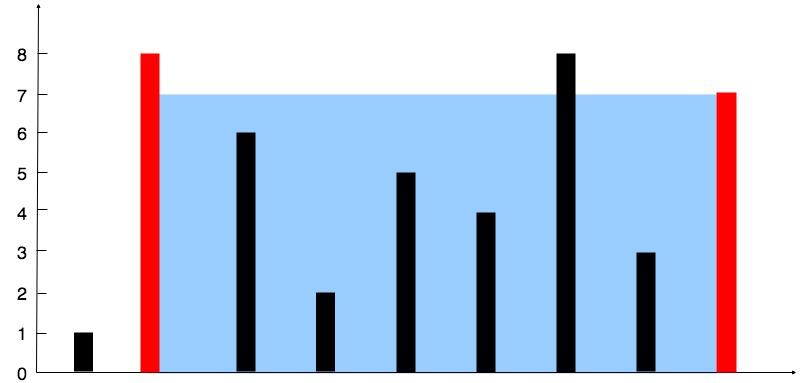
height = [1,8,6,2,5,4,8,3,7]
Output:
49
Explanation:
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example 2:
Input:
height = [1,1]
Output:
1
Think First
We need to find the container with the most water, which is in terms of an optimization problem. A greedy Algorithm can do wonders here.
To do this problem we will combine two techniques: two-pointers and greedy strategy. By observation, we can easily calculate the amount of water between any two lines by doing area (i2-i1) x min ( a1,a2). Firstly, we will have two values left and right, left = the first position of height array and right = last position of height array. We will assume that the max area must have the max (right-left) first then each time we calculate (right-left) * min(a[right],a[left]) and update our result. At each step, we will eliminate the min-height,
for example :
if a[right] < a[left] then r--
elst left ++
It is because the area will be limited by the greater value so if a < b and we eliminate b then the area will be limited by a then the next area we calculate will be (right-left) x c ( c<=a ) but if we eliminate a then the next area we calculate will be (right-left) x c ( c<=b ). This is the reason why the greedy strategy works.
Time Complexity
We just go through all the elements of the height array so the time complexity is O(n).Space Complexity
Because we use a constant number of variables so the space complexity is O(1).
Solution :
class Solution {
public:
int maxArea(vector<int>& height) {
int res=0,n=height.size()-1;
int l=0, r=n,tmp;
while (l<r) {
tmp = min(height[l],height[r]);
if ((r-l)*tmp>res) res = (r-l)*tmp;
if (tmp==height[r]) --r;
else ++l;
}
return res;
}
};Hope your first day was good enough to learn a new skill.
This problem has been taken from here1, don’t forget to submit your solution.
Thank you!
https://leetcode.com/problems/container-with-most-water/